跳转至

堆

堆是一种特别的二叉树，满足以下条件的二叉树，可以称之为堆： 1. 完全二叉树； 2. 每一个节点的值都必须大于等于或者小于等于其孩子节点的值。

堆具有以下的特点： * 可以在 \(O(log{}N)\) 的时间复杂度内向堆中插入元素； * 可以在 \(O(log{}N)\) 的时间复杂度内向堆中删除元素； * 可以在 \(O(1)\) 的时间复杂度内获取堆中的最大值或最小值。

堆的分类

最大堆：堆中每一个节点的值都大于等于其孩子节点的值。所以最大堆的特性是堆顶元素（根节点）是堆中的最大值。 最小堆：堆中每一个节点的值都小于等于其孩子节点的值。所以最小堆的特性是 堆顶元素（根节点）是堆中的最小值。

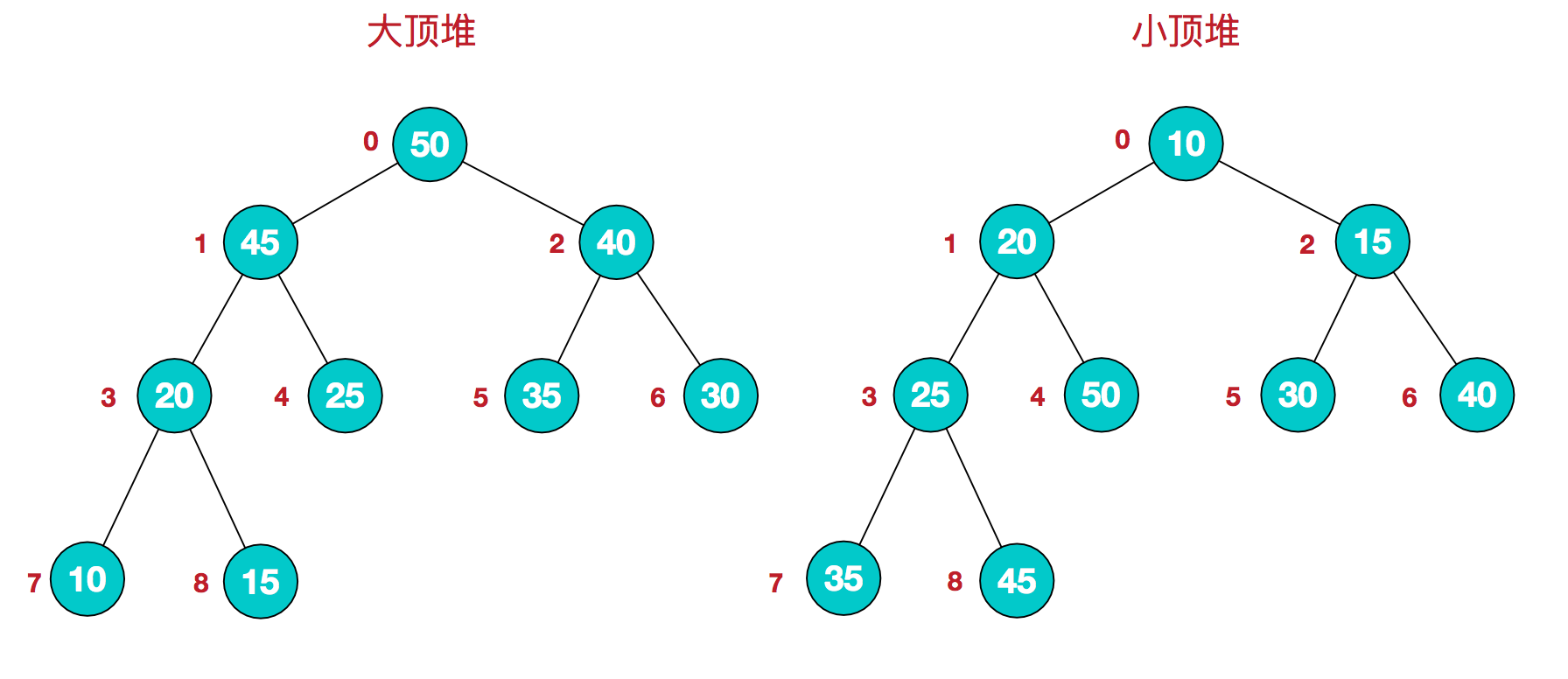
Pasted image 20221029114514.png

对堆中的结点按层进行编号：

Pasted image 20221029114604.png

完全二叉树与数组的关联

堆是完全二叉树，对于一个完全二叉树，可以使用数组来表示。假设完全二叉树中有 n 个节点，将这些节点按照树的层次遍历顺序依次放入数组中，根节点放在数组下标为 1 的位置，其左孩子放在下标为 2 的位置，右孩子放在下标为 3 的位置，以此类推。

       1
     /   \
    2     3
   / \   /
  4   5  6

对应的数组表示为：[1, 2, 3, 4, 5, 6]。其中，数组的第一个元素就是根节点，而后面的元素按照层次遍历的顺序依次排列。

利用数组表示完全二叉树有以下优点：

  1. 索引计算方便：给定一个节点在数组中的索引 \(i\)，可以通过简单的计算得到它的父节点、左孩子和右孩子在数组中的位置。父节点的索引为 \(i/2\)，左孩子的索引为 \(2i\)，右孩子的索引为 \(2i+1\)。对于有 \(n\) 个元素的完全二叉树（\(n>2\)），它的最后一个非叶子结点的下标：\(n/2 - 1\)。
  2. 节省空间：相比于使用指针来表示节点间的连接关系，数组表示使用的空间更少。

需要注意的是，当完全二叉树中的节点不满时，数组中可能会存在一些无效的空间。一般来说，可以使用 -1 或者 null 来表示这些空间。

代码实现（基于数组）
class MaxHeap {
public:
    MaxHeap(int _totalSize) {
        _size = 0;
        _totalSize = _totalSize;
        _data = new int[_totalSize + 1];
    };
    ~MaxHeap() {
        delete[] _data;
    }
    bool push(int element) {
        _size++;
        if (_size > _totalSize) {
            _size--;
            return false;
        }
        _data[_size] = element;
        int index = _size;
        int parent = _size / 2;
        while (_data[index] > _data[parent] && index > 1) {
            swap(_data[index], _data[parent]);
            index = parent;
            parent = index / 2;
        }
        return true;
    }
    bool pop() {
        if (_size < 1) {
            return false;
        }
        _data[1] = _data[_size];
        _size--;
        int index = 1;
        while (index < _size && index <= _size / 2) {
            int leftChildIndex = index * 2;
            int rightChildIndex = index * 2 + 1;
            if (_data[index] < _data[leftChildIndex] || _data[index] <  _data[rightChildIndex]) {
                if (_data[leftChildIndex] > _data[rightChildIndex]) {
                    swap(_data[leftChildIndex], _data[index]);
                    index = leftChildIndex;
                } else {
                    swap(_data[rightChildIndex], _data[index]);
                    index = rightChildIndex;
                }
            } else {
                break;
            }
        }
        return true;
    }
    int size() {
        return _size;
    }
    int top() {
        if (_size == 0) return INT_MIN;
        return _data[1];
    }
private:
    int _size;
    int _totalSize;
    int * _data;
};

多种语言中实现了优先队列，其底层数据结构就是堆数据结构。C++ 可直接使用 priority_queue。