希尔排序

希尔排序最初在 1959 年 7 月由美国辛辛那提大学的数学系博士唐纳德·希尔（Donald Shell）在《ACM 通讯》上发表，希尔排序是首批将时间复杂度降到 \(O(n^2)\) 的排序算法之一。虽然原始的希尔排序最坏时间复杂度仍然是 \(O(n^2)\)，但经过优化的希尔排序可以达到 \(O(n^{1.3})\) 甚至 \(O(n^{7/6})\)。

基本思想

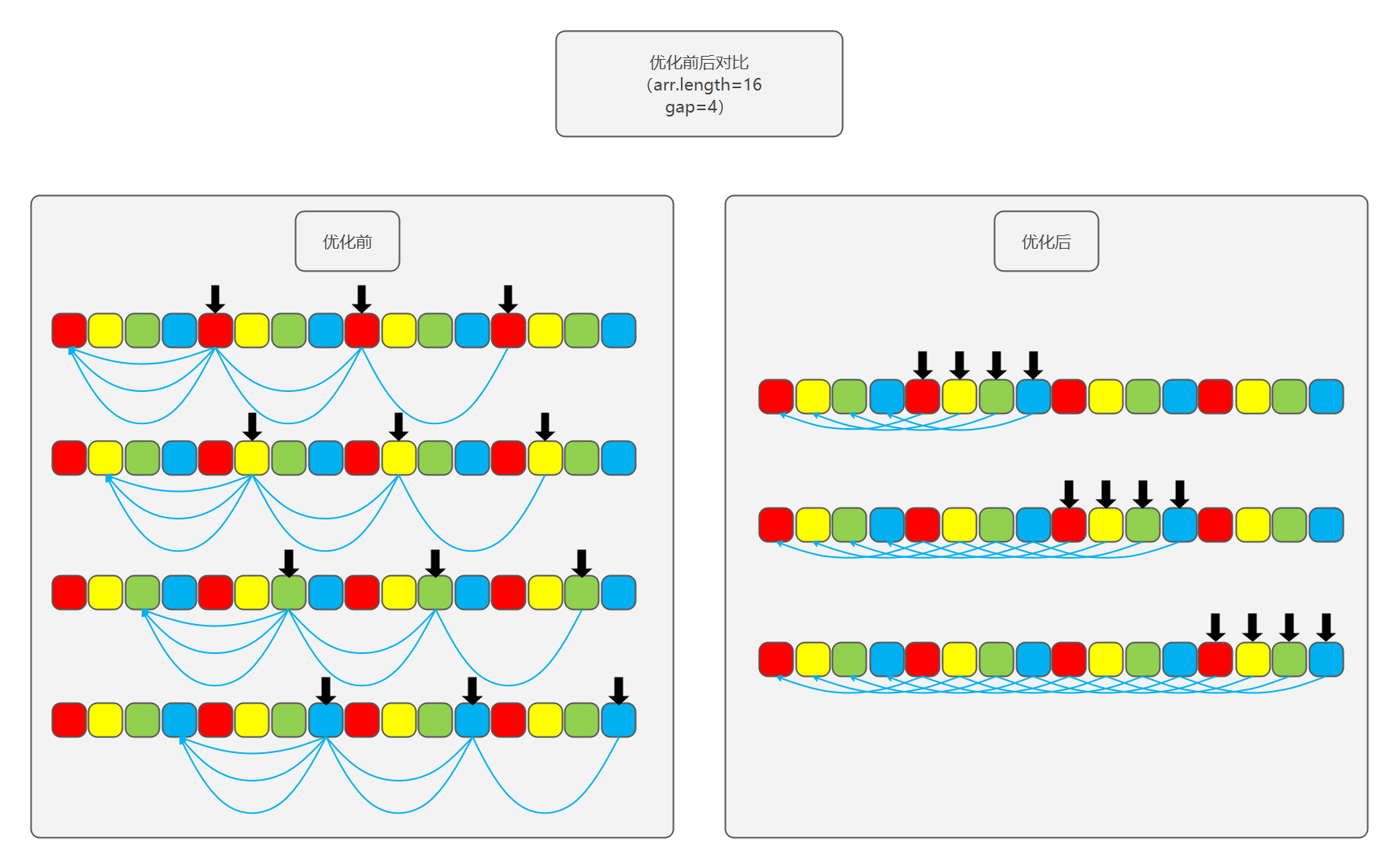
希尔排序本质上是对插入排序的一种优化，它利用了插入排序的简单，又克服了插入排序每次只交换相邻两个元素的缺点。它的基本思想是：

• 将待排序数组按照一定的间隔分为多个子数组，每组分别进行插入排序。这里按照间隔分组指的不是取连续的一段数组，而是每跳跃一定间隔取一个值组成一组；
• 逐渐缩小间隔进行下一轮排序；
• 最后一轮时，取间隔为 \(1\)，也就相当于直接使用插入排序。但这时经过前面的「宏观调控」，数组已经基本有序了，所以此时的插入排序只需进行少量交换便可完成。

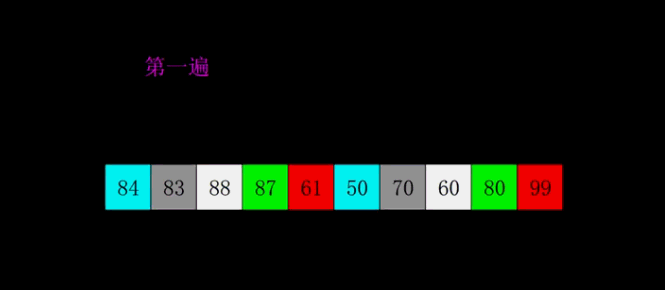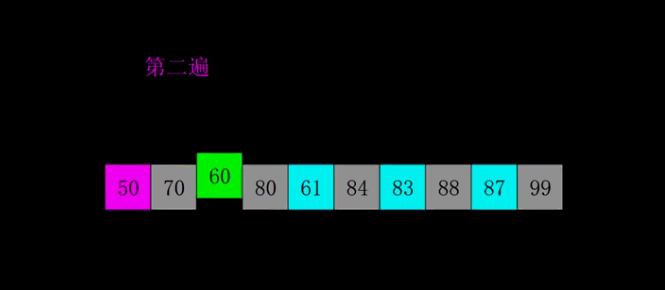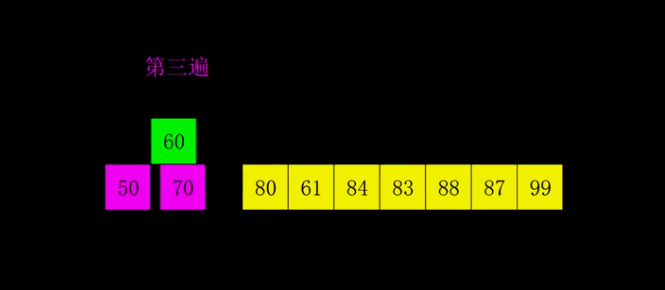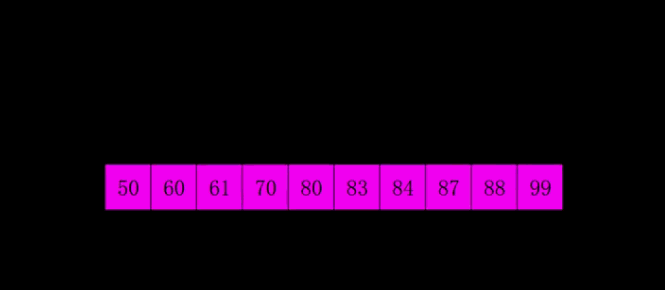
每一遍排序的间隔在希尔排序中被称之为增量，所有的增量组成的序列称之为增量序列。增量依次递减，最后一个增量必须为 \(1\)，所以希尔排序又被称之为缩小增量排序。要是以专业术语来描述希尔排序，可以分为以下两个步骤：

• 定义增量序列 *\(D_m > D_{m-1} > D_{m-2} > ... > D_1 = 1\)；
• • 对每个 \(D_k\) 进行 「\(D_k\)​ 间隔排序」。

增量序列的选择会极大地影响希尔排序的效率。一个简单的增量序列为 \(D_m = N/2, D_k = D_{k+1} / 2\)，这个序列正是当年希尔发表此算法的论文时选用的序列，所以也被称之为希尔增量序列。

代码实现

这里以希尔发表此算法的论文时选用的增量序列 \(D_m = N/2, D_k = D_{k+1} / 2\) 为例，这个增量序列也被称为希尔增量序列。希尔排序的代码写法分两种版本，分别适合人类思维（基础版本）和符合计算机运行逻辑（优化版本）。注意，这里的优化指的是代码复杂程度上的优化，实际上两个版本的运行效率几乎一样。

基础版本

class Solution {
public:
    vector<int> shellSortBasic(vector<int>& nums) {
        for (int gap = nums.size() / 2; gap >= 1; gap /= 2) {
            for (int start = 0; start < gap; start++) {
                for (int current = start + gap; current < nums.size(); current += gap) {
                    int currentNum = nums[current];
                    int pre = current - gap;
                    while (pre >= 0 && currentNum < nums[pre]) {
                        nums[pre + gap] = nums[pre];
                        pre -= gap;
                    }
                    nums[pre + gap] = currentNum;
                }
            }
        }
        return nums;
    }
};

优化版本

class Solution {
public:
    vector<int> shellSortOptimized(vector<int>& nums) {
        for (int gap = nums.size() / 2; gap >= 1; gap /= 2) {
            for (int i = gap; i < nums.size(); i++) {
                int num = nums[i];
                int pre = i - gap;
                while (pre >= 0 && num < nums[pre]) {
                    nums[pre + gap] = nums[pre];
                    pre -= gap;
                }
                nums[pre + gap] = num;
            }
        }
        return nums;
    }
};

增量序列的选择

前面提到，增量序列的选择会极大地影响希尔排序的效率。希尔排序的增量序列如何选择是一个数学界的难题，但它也是希尔排序算法的核心优化点。数学界有不少的大牛做过这方面的研究。比较著名的有 Hibbard 增量序列、Knuth 增量序列、Sedgewick 增量序列。

• Hibbard 增量序列：\(D_k = 2^k - 1\)，也就是 \({1, 3, 7, 15, ...}\)。数学界猜想它最坏的时间复杂度为 \(O(n^{3/2})\)，平均时间复杂度为 \(O(n^{5/4})\)；
• Knuth 增量序列：\(D_1 = 1; D_{k+1} = 3 * D_k + 1\)，也就是 \({1, 4, 13, 40, ...}\)，数学界猜想它的平均时间复杂度为 \(O(n^{3/2})\)；
• Sedgewick 增量序列： \({1, 5, 19, 41, 109, ...}\)，这个序列的元素有的是通过 \(9 * 4^k - 9 * 2^k + 1\) 计算出来的，有的是通过 \(4^k - 3 * 2^k + 1\) 计算出来的。数学界猜想它最坏的时间复杂度为 \(O(n^{4/3})\)，平均时间复杂度为 \(O(n^{7/6})\)。

希尔排序与 \(O(n^2)\) 级排序算法的本质区别

排序算法本质上就是一个消除逆序对的过程。对于逆序对，通俗来讲就是———当我们从小到大排序时，在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。

对于随机数组，逆序对的数量是 \(O(n^2)\) 级的，如果采用「交换相邻元素」的办法来消除逆序对，每次最多只能消除一组逆序对，因此必须执行 \(O(n^2)\) 级的交换次数，这就是为什么冒泡、插入、选择算法只能到 \(O(n^2)\) 级的原因。反过来说，基于交换元素的排序算法要想突破 \(O(n^2)\) 级，必须通过一些比较，交换间隔比较远的元素，使得一次交换能消除一个以上的逆序对。

希尔排序算法就是通过这种方式，打破了在空间复杂度为 \(O(1)\) 的情况下，时间复杂度为 \(O(n^2)\) 的魔咒，此后的快排、堆排等等算法也都是基于这样的思路实现的。

• https://leetcode.cn/leetbook/read/sort-algorithms/eu039h/