并查集
并查集(英文:Disjoint Set Union (DSU),直译为不交集数据结构,一般叫做不相交集合)是一种数据结构),用于管理元素所属集合的数据结构,通常实现为一个森林(一组树结构),其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
并查集支持如下操作:
- 查询(Find):查询某个元素属于哪个集合,通常是返回集合内的一个“代表元素”。这个操作是为了判断两个元素是否在同一个集合之中。(并查集只知道两个顶点之间是否有一条路径连接,而不知道如何连接)
- 合并(Union):将两个集合合并为一个。
- 添加:添加一个新集合,其中有一个新元素。添加操作不如查询和合并操作重要,常常被忽略。
由于支持查询和合并这两种操作,并查集在英文中也被称为联合-查找数据结构(Union-find data structure)或者合并-查找集合(Merge-find set)。
“并查集”可以用来指代任何支持上述操作的数据结构,但是一般来说,“并查集”特指其中最常见的一种实现:不交集森林(Disjoint-set forest)。经过优化的不交集森林有线性的空间复杂度(\(O(n)\),\(n\) 为元素数目,下同),以及接近常数的单次操作平均时间复杂度(\(O(\alpha(n))\),\(\alpha\) 为反阿克曼函数),是效率最高的常见数据结构之一。
很多数据结构都因为具有 动态 处理问题的能力而变得高效,例如「堆」「二叉查找树」等。所谓「动态」的意思是:要处理的数据不是一开始就确定好的,理解「并查集」动态处理数据的最好的例子是「最小生成树」算法。
可以使用并查集的问题一般都可以使用基于遍历的搜索算法(深度优先搜索、广度优先搜索)完成,但是使用并查集会使得解决问题的过程更加清晰、直观。
并查集只回答两个节点是不是在同一个连通分量中(也就是所谓的连通性问题),而并不回答路径问题。
可以使用「并查集」解决的问题,一般都可以使用「深度优先搜索」和「广度优先搜索」完成。但是「深度优先搜索」和「广度优先搜索」不仅回答了连接问题,还回答了路径问题,时间复杂度高。有一些问题恰恰好只需要我们回答连通性问题,这样的问题是应用「并查集」的典型问题。
实现¶
并查集有两种实现思路:
quick-find基于 id- 相同的集合分配一个唯一的标识,称为 id;
- 初始化:所有元素的 id 都不同,表示每个元素单独属于一个集合;
- 不同元素如果 id 相同,表示属于同一个集合;
- 查询时可直接得知属于哪个集合;
- 合并集合时,将被合并的所有元素的 id 设置为目标集合的 id。
quick-union基于 parent- 只记录节点(元素)属于哪一个父亲节点,这样设计「并查集」的思想也叫「代表元」法;
- 查询时需要不断向上查找父亲节点,直到找到根节点,如果根节点相同,表示属于同一个集合;
- 合并时只需要将被合并元素的根节点的父亲节点设置为目标集合的根节点;
- 从总体上来说,这种结构和树结构相似,只不过前者从下往上访问,而后者从上往下访问。
用集合中的某个元素来代表这个集合,该元素称为集合的代表元。
代表元法¶
代表元的三个不重要: * 谁作为根结点不重要:根结点与非根结点只是位置不同,并没有附加的含义; * 树怎么形成的不重要:合并的时候任何一个集合的根结点指向另一个结合的根结点就可以; * 树的形态不重要:理由同「谁作为根结点不重要」。
代表元法可能造成的问题:树的高度过高,查询性能降低。可以通过一定规则的合并(按秩合并)和路径压缩来优化这个问题。
知识扩展:几乎所有的「树」的问题都在和「树的高度」较劲: 「快速排序」,使用随机化 pivot 的方式避免递归树太深; 「二叉搜索树」为了避免递归树太深,采用不同的旋转方式,得到了 AVL 树和红黑树。
A. 按秩合并¶
按秩合并的意思是:让树的秩较小的树的根结点,指向树的秩较大的树的根结点。
这里的「秩」有两种含义,分别用于不同的场景:
- 按 size 合并,用于需要维护每个连通分量结点个数的时候;
- 按 rank 合并,绝大多数时候。这里的 rank 指的是树的(大致)高度。
B. 路径压缩¶
把从查询结点到根结点沿途经过的所有结点全部修改指向根结点。或者也可以选择部分压缩,两步一跳,或者三步一跳,这样可以减少单次合并操作可能的最大耗时。
复杂度¶
在同时使用按秩合并与路径压缩时,并查集合并的时间复杂度为 \(O(\alpha(n))\),这里 \(\alpha(n)\) 是一个增长非常慢的函数,\(\alpha(n) \le 4\)。并查集查询的时间复杂度为 \(O(h)\),这里 \(h\) 为树的高度。
代码实现¶
class Dsu {
public:
Dsu(size_t n): parents(n), sizes(n, 1) {
iota(parents.begin(), parents.end(), 0);
}
void unite(int a, int b) {
if (a == b) return;
int rootA = find(a);
int rootB = find(b);
if (rootA == rootB) return;
if (sizes[rootA] < sizes[rootB]) {
parents[rootA] = rootB;
sizes[rootB] += sizes[rootA];
} else {
parents[rootB] = rootA;
sizes[rootA] += sizes[rootB];
}
}
int find(int a) {
if (parents[a] != a) {
parents[a] = find(parents[a]);
}
return parents[a];
}
private:
vector<int> parents;
vector<int> sizes;
};
带权并查集¶
在「查询」操作的「路径压缩」优化中维护权值变化¶
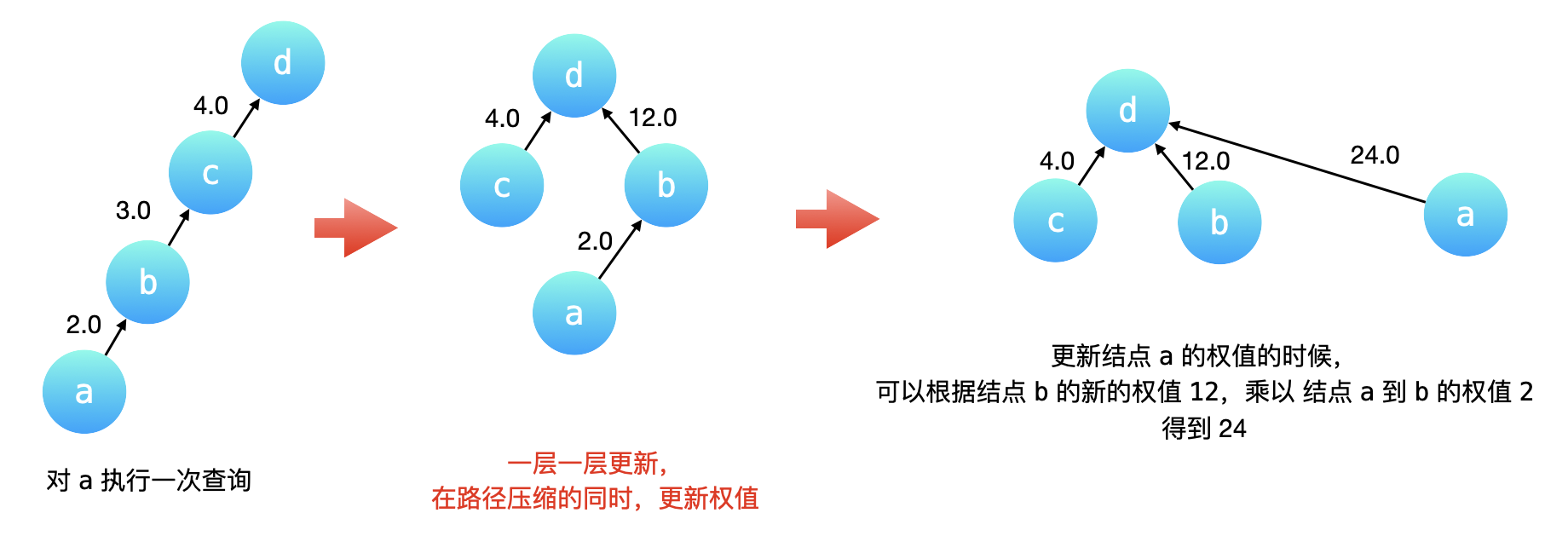
如下图所示,我们在结点 a 执行一次「查询」操作。路径压缩会先一层一层向上先找到根结点 d,然后依次把 c、b 、a 的父亲结点指向根结点 d。
- c 的父亲结点已经是根结点了,它的权值不用更改;
- b 的父亲结点要修改成根结点,它的权值就是从当前结点到根结点经过的所有有向边的权值的乘积,因此是 \(3.0\) 乘以 \(4.0\) 也就是 \(12.0\);
- a 的父亲结点要修改成根结点,它的权值就是依然是从当前结点到根结点经过的所有有向边的权值的乘积,但是我们没有必要把这三条有向边的权值乘起来,这是因为 b 到 c,c 到 d 这两条有向边的权值的乘积,我们在把 b 指向 d 的时候已经计算出来了。因此,a 到根结点的权值就等于 b 到根结点 d 的新的权值乘以 a 到 b 的原来的有向边的权值。
如何在「合并」操作中维护权值的变化¶
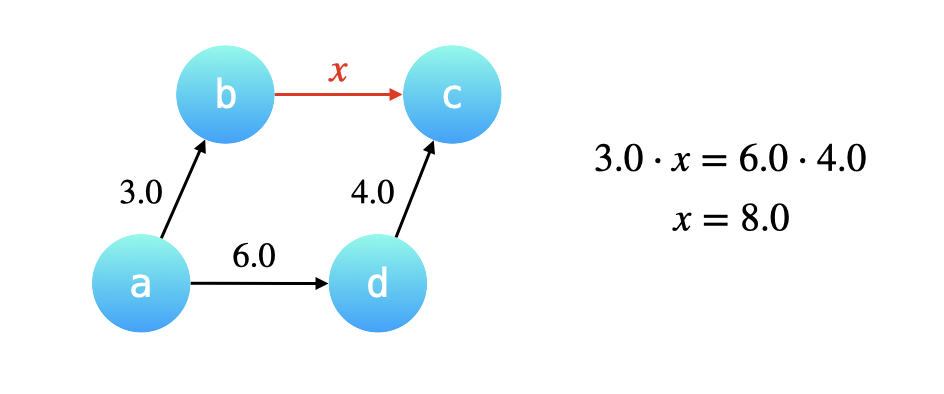
「合并」操作基于这样一个 很重要的前提:我们将要合并的两棵树的高度最多为 \(2\),换句话说两棵树都必需是「路径压缩」以后的效果,两棵树的叶子结点到根结点最多只需要经过一条有向边。
例如已知 \(a\stackrel{3.0}{\longrightarrow}b\),\(d\stackrel{4.0}{\longrightarrow}c\),又已知 \(a\stackrel{6.0}{\longrightarrow}d\),现在合并结点 a 和 d 所在的集合,其实就是把 a 的根结点 b 指向 d 的根结 c,那么如何计算 b 指向 c 的这条有向边的权重呢?
根据 a 经过 b 可以到达 c,a 经过 d 也可以到达 c,因此 两条路径上的有向边的权值的乘积是一定相等的。设 b 到 c 的权值为 \(x\),那么 \(3.0⋅x=6.0⋅4.0\) ,得 \(x=8.0\)。
代码实现¶
class WeightedDsu {
public:
WeightedDsu(size_t n): parents(n), sizes(n, 1), weights(n, 1.0) {
iota(parents.begin(), parents.end(), 0);
}
void unite(int a, int b, double value) {
if (a == b) return;
int rootA = find(a);
int rootB = find(b);
if (rootA == rootB) return;
if (sizes[rootA] < sizes[rootB]) {
parents[rootA] = rootB;
weights[rootA] = weights[b] * value / weights[a];
sizes[rootB] += sizes[rootA];
} else {
parents[rootB] = rootA;
weights[rootB] = weights[a] / (weights[b] * value);
sizes[rootA] += sizes[rootB];
}
}
int find(int a) {
if (parents[a] != a) {
int origin = parents[a];
parents[a] = find(parents[a]);
weights[a] *= weights[origin];
}
return parents[a];
}
double weight(int a) {
return weights[a];
}
private:
vector<int> parents;
vector<int> sizes;
vector<double> weights;
};
可变长度版¶
parents 和 sizes 都使用 unordered_map 类型,在调用 find 方法时,动态添加新元素。
class DynamicDsu {
public:
DynamicDsu() {
count = 0;
}
void unite(int a, int b) {
if (a == b) return;
int rootA = find(a);
int rootB = find(b);
if (rootA == rootB) return;
if (sizes[rootA] < sizes[rootB]) {
parents[rootA] = rootB;
sizes[rootB] += sizes[rootA];
} else {
parents[rootB] = rootA;
sizes[rootA] += sizes[rootB];
}
count--;
}
int find(int a) {
if (parents.count(a) == 0) {
parents[a] = a;
sizes[a] = 1;
count++;
return a;
}
if (parents[a] != a) {
parents[a] = find(parents[a]);
}
return parents[a];
}
int findOrCreate(int a) {
if (parents[a] != a) {
parents[a] = find(parents[a]);
}
return parents[a];
}
int getCount() {
return count;
}
private:
int count;
unordered_map<int, int> parents;
unordered_map<int, int> sizes;
};