树的最近公共祖先算法
最近公共祖先,简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 为了方便,我们记某点集 \(S=\{v_1,v_2,\ldots,v_n\}\) 的最近公共祖先为 \(\text{LCA}(v_1,v_2,\ldots,v_n)\) 或 \(\text{LCA}(S)\)。
性质¶
节选翻译自 PEGWiki - Lowest common ancestor
- \(\text{LCA}(\{u\})=u\);
- \(u\) 是 \(v\) 的祖先,当且仅当 \(\text{LCA}(u,v)=u\);
- 如果 \(u\) 不为 \(v\) 的祖先并且 \(v\) 不为 \(u\) 的祖先,那么 \(u,v\) 分别处于 \(\text{LCA}(u,v)\) 的两棵不同子树中;
- 前序遍历中,\(\text{LCA}(S)\) 出现在所有 \(S\) 中元素之前,后序遍历中 \(\text{LCA}(S)\) 则出现在所有 \(S\) 中元素之后;
- 两点集并的最近公共祖先为两点集分别的最近公共祖先的最近公共祖先,即 \(\text{LCA}(A\cup B)=\text{LCA}(\text{LCA}(A), \text{LCA}(B))\);
- 两点的最近公共祖先必定处在树上两点间的最短路上;
- \(d(u,v)=h(u)+h(v)-2h(\text{LCA}(u,v))\),其中 \(d\) 是树上两点间的距离,\(h\) 代表某点到树根的距离。
求法¶
朴素算法¶
可以每次找深度比较大的那个点,让它向上跳。显然在树上,这两个点最后一定会相遇,相遇的位置就是想要求的 LCA。或者先向上调整深度较大的点,令他们深度相同,然后再共同向上跳转,最后也一定会相遇。朴素算法预处理时需要深度优先搜索整棵树,时间复杂度为 \(O(n)\),单次查询时间复杂度为 \(\Theta(n)\)。但由于随机树高为 \(O(\log n)\),所以朴素算法在随机树上的单次查询时间复杂度为 \(O(\log n)\)。
倍增算法¶
过程¶
倍增算法(inary Lifting)是最经典的 LCA 求法,他是朴素算法的改进算法。
一个初步的想法是,预处理出每个节点的「爷爷节点」,即父节点的父节点,那么就可以两步两步地往上跳,从而减少一半的跳跃次数(循环次数);进一步地,再预处理出爷爷节点的爷爷节点,就可以四步四步地往上跳;以此类推,即预先计算好每个节点的上一辈祖先,上两辈祖先,上四辈祖先,上八辈祖先,….,上 \(2^k\) 辈祖先,\(k=\log_2(n)\)。
预处理出每个节点的第 \(2^i\) 个祖先节点,即第 \(2,4,8,\cdots\) 个祖先节点(注意 \(x\) 的第 \(1\) 个祖先节点就是 \(\textit{parent}[x]\))。由于任意 \(k\) 可以分解为若干不同的 \(2\) 的幂(例如 \(69=64+4+1\)),所以只需要预处理出这些 \(2^i\) 祖先节点,就可以快速地到达任意第 \(k\) 个祖先节点。
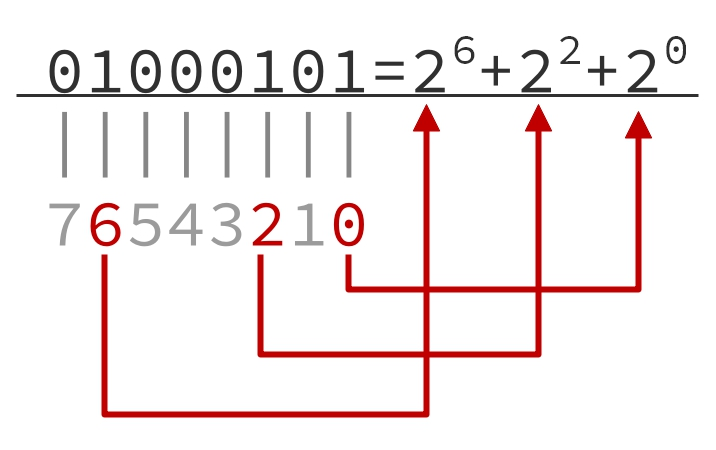
例如 \(k=69=64+4+1=01000101_{(2)}\),可以先往上跳 \(64\) 步,再往上跳 \(4\) 步和 \(1\) 步;也可以先往上跳 \(1\) 步,再往上跳 \(4\) 步和 \(64\) 步。无论如何跳,都只需要跳 \(3\) 次就能到达第 \(69\) 个祖先节点。
性质¶
倍增算法的预处理时间复杂度为 \(O(n \log n)\),单次查询时间复杂度为 \(O(\log n)\)。
另外倍增算法可以通过交换 ancestors 数组的两维使较小维放在前面。这样可以减少缓存未命中的次数,提高程序效率。
https://oi-wiki.org/graph/lca/ https://shawnliang.wiki/post/lca-binary-lifting/