快速排序

快速排序算法由东尼·霍尔（C. A. R. Hoare）在 1960 年提出。快速排序采用分治思想，其基本思想是：

从数组中取出一个数，称之为基数（pivot）；
遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域；
将左右两个区域视为两个数组，重复前两个步骤，直到排序完成。

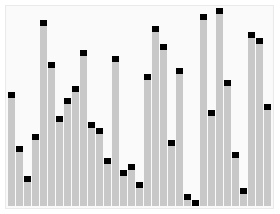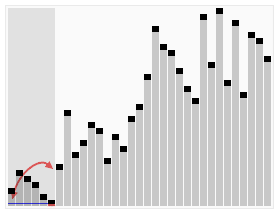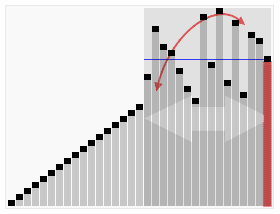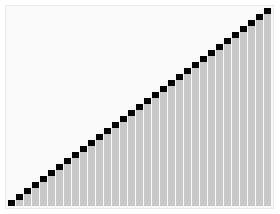
代码实现的基本框架¶

class Solution {
public:
    void quickSort(vector<int>& nums) {
        _quickSortHelper(nums, 0, nums.size() - 1);
    }
    void _quickSortHelper(vector<int>& nums, int start, int end) {
        if (end - start < 2) return;
        int mid = _partition(nums, start, end);
        _quickSortHelper(nums, start, mid - 1);
        _quickSortHelper(nums, mid + 1, end);
    }
    int _partition(vector<int>& nums, int start, int end) {
        // TODO: implement this
        // selection of pivot
        // partition algorithm
    }
};

基数的选择¶

基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。通常来讲有三种选择方式：

选择第一个元素作为基数；
选择最后一个元素作为基数；
选择区间内一个随机元素作为基数。

最简单的分区算法¶

分区的方式也有很多种，最简单的思路是：从 left 开始，遇到比基数大的数，就交换到数组最后，并将 right 减一，直到 left 和 right 相遇，此时数组就被分成了左右两个区域。再将基数和中间的数交换，返回中间值的下标即可。

    int _partition(vector<int>& nums, int start, int end) {
        int pivot = nums[0];
        int left = start + 1;
        int right = end;
        while (left < right) {
            if (nums[left] > pivot) {
                swap(nums[left], nums[right]);
                right--;
            } else {
                left++;
            }
        }
        if (left == right && nums[right] > pivot) right--;
        if (right != start) swap(nums[right], nums[start]);
        return right;
    }

双指针分区算法¶

双指针的分区算法更为常用：从 left 开始，遇到比基数大的数，记录其下标；再从 right 往前遍历，找到第一个比基数小的数，记录其下标；然后交换这两个数。继续遍历，直到 left 和 right 相遇。然后就和刚才的算法一样了，交换基数和中间值，并返回中间值的下标。

    int _partition(vector<int>& nums, int start, int end) {
        int pivot = nums[0];
        int left = start + 1;
        int right = end;
        while (left < right) {
            while (left < right && nums[left] <= pivot) left++;
            while (left < right && nums[right] >= pivot) right--;
            if (left < right) {
                swap(nums[left], nums[right]);
                left++;
                right--;
            }
        }
        if (left == right && nums[right] > pivot) right--;
        if (right != start) swap(nums[right], nums[start]);
        return right;
    }

三区间双指针分区算法（三路快速排序）¶

相比于双指针分区算法，由 pivot 分割出的两个区间（小于等于 pivot 、大于等于 pivot ）变为三个区间（小于 pivot、等于 pivot、大于 pivot）。这个分区算法对于选中的 pivot 有大量相同元素的情况，递归区间会大大减少，极大提高了效率。

    void _quickSortHelper(vector<int>& nums, int start, int end) {
        if (start >= end) return;
        auto range = _partition(nums, start, end);
        _quickSortHelper(nums, start, range.first);
        _quickSortHelper(nums, range.second, end);
    }
    pair<int, int> _partition(vector<int>& nums, int start, int end) {
        swap(nums[start], nums[start + (rand() % (end - start))]);
        int pivot = nums[start];
        // range { n < nums[pivot] }: [start, left)
        // range { n == nums[pivot] }: [left, right]
        // range { n > nums[pivot] }: (right, end]
        int left = start;
        int right = end;
        int i = left + 1;
        while (i <= right) {
            if (nums[i] < pivot) {
                swap(nums[i], nums[left]);
                left++;
                i++;
            } else if (nums[i] > pivot) {
                swap(nums[i], nums[right]);
                right--;
            } else {
                i++;
            }
        }
        return make_pair(left-1, right+1);
    }

完整代码实现（随机基数、三指针）¶

class Solution {
public:
    void quickSort(vector<int>& nums) {
        _quickSortHelper(nums, 0, nums.size() - 1);
    }
    void _quickSortHelper(vector<int>& nums, int start, int end) {
        if (start >= end) return;
        auto range = _partition(nums, start, end);
        _quickSortHelper(nums, start, range.first);
        _quickSortHelper(nums, range.second, end);
    }
    pair<int, int> _partition(vector<int>& nums, int start, int end) {
        swap(nums[start], nums[start + (rand() % (end - start))]);
        int pivot = nums[start];
        int left = start;
        int right = end;
        int i = left + 1;
        while (i <= right) {
            if (nums[i] < pivot) {
                swap(nums[i], nums[left]);
                left++;
                i++;
            } else if (nums[i] > pivot) {
                swap(nums[i], nums[right]);
                right--;
            } else {
                i++;
            }
        }
        return make_pair(left-1, right+1);
    }
};

https://leetcode.cn/leetbook/read/sort-algorithms/eul7hm/
https://zh.wikipedia.org/zh-hans/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F
https://oi-wiki.org/basic/quick-sort/